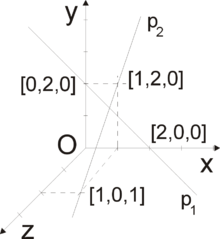
Rovnoběžky p1 a p2 . Různoběžky p1 a p2 s průsečíkem P. Mimoběžky p1 a p2 . Rovnoběžky v rovině jsou přímky , které mají stejný směr a nemají žádný společný bod . Speciálním případem je totožnost . Dále různoběžky jsou přímky, které se protínají právě v jednom bodě – průsečíku . Ten je tedy jejich jediným společným bodem.
Mějme dvě přímky v rovině dané směrnicovými rovnicemi
y
=
k
1
x
+
q
1
{\displaystyle y=k_{1}x+q_{1}}
y
=
k
2
x
+
q
2
{\displaystyle y=k_{2}x+q_{2}}
popř. obecnými rovnicemi
a
1
x
+
b
1
y
+
c
1
=
0
{\displaystyle a_{1}x+b_{1}y+c_{1}=0}
a
2
x
+
b
2
y
+
c
2
=
0
{\displaystyle a_{2}x+b_{2}y+c_{2}=0}
Dvě přímky v rovině jsou rovnoběžné , pokud mají stejné směrnice . Jsou-li tedy dvě přímky zadány směrnicovými rovnicemi, pak podmínka rovnoběžnosti má tvar
k
1
=
k
2
{\displaystyle k_{1}=k_{2}}
Jsou-li přímky zadány obecnými rovnicemi, pak podmínku rovnoběžnosti lze vyjádřit pomocí determinantu jako
|
a
1
b
1
a
2
b
2
|
=
a
1
b
2
−
a
2
b
1
=
0
{\displaystyle {\begin{vmatrix}a_{1}&b_{1}\\a_{2}&b_{2}\end{vmatrix}}=a_{1}b_{2}-a_{2}b_{1}=0}
Přímky zadané rovnicemi směrnicovými rovnicemi jsou kolmé , pokud jejich směrnice splňují podmínku
k
1
k
2
+
1
=
0
{\displaystyle k_{1}k_{2}+1=0}
k
1
=
−
1
k
2
{\displaystyle k_{1}=-{\frac {1}{k_{2}}}}
Rovnice zadané v obecném tvaru jsou kolmé pokud splňují podmínku
a
1
a
2
+
b
1
b
2
=
0
{\displaystyle a_{1}a_{2}+b_{1}b_{2}=0}
Průsečík dvou přímek zadaných směrnicovými rovnicemi získáme řešením této soustavy , čímž dostaneme souřadnice průsečíku
x
P
=
q
1
−
q
2
k
2
−
k
1
{\displaystyle x_{P}={\frac {q_{1}-q_{2}}{k_{2}-k_{1}}}}
y
P
=
q
1
k
2
−
q
2
k
1
k
2
−
k
1
{\displaystyle y_{P}={\frac {q_{1}k_{2}-q_{2}k_{1}}{k_{2}-k_{1}}}}
Podobně pro průsečík přímek zadaných obecnými rovnicemi dostaneme
x
P
=
|
b
1
c
1
b
2
c
2
|
|
a
1
b
1
a
2
b
2
|
{\displaystyle x_{P}={\frac {\begin{vmatrix}b_{1}&c_{1}\\b_{2}&c_{2}\end{vmatrix}}{\begin{vmatrix}a_{1}&b_{1}\\a_{2}&b_{2}\end{vmatrix}}}}
y
P
=
|
c
1
a
1
c
2
a
2
|
|
a
1
b
1
a
2
b
2
|
{\displaystyle y_{P}={\frac {\begin{vmatrix}c_{1}&a_{1}\\c_{2}&a_{2}\end{vmatrix}}{\begin{vmatrix}a_{1}&b_{1}\\a_{2}&b_{2}\end{vmatrix}}}}
Z předchozích vztahů je vidět, že pokud je splněna podmínka rovnoběžnosti, tak přímky jsou rovnoběžné a nemají tedy průsečík.
Odchylka
φ
{\displaystyle \varphi }
různoběžných přímek zadaných směrnicovými rovnicemi je pro
k
1
k
2
≠
−
1
{\displaystyle k_{1}k_{2}\neq -1}
tg
φ
=
|
k
2
−
k
1
1
+
k
1
k
2
|
{\displaystyle \operatorname {tg} \varphi =\left|{\frac {k_{2}-k_{1}}{1+k_{1}k_{2}}}\right|}
Jsou-li rovnice zadány obecnými rovnicemi, pak pro odchylku dostáváme
tg
φ
=
|
a
1
b
2
−
a
2
b
1
a
1
a
2
+
b
1
b
2
|
{\displaystyle \operatorname {tg} \varphi =\left|{\frac {a_{1}b_{2}-a_{2}b_{1}}{a_{1}a_{2}+b_{1}b_{2}}}\right|}
pro
a
1
a
2
+
b
1
b
2
≠
0
{\displaystyle a_{1}a_{2}+b_{1}b_{2}\neq 0}
Rovnoběžky v prostoru jsou přímky, které mají stejný směr. Speciálním případem jsou totožné přímky. Dále různoběžky jsou přímky, které se protínají právě v jednom bodě, tedy mají právě jeden společný bod. Mimoběžky jsou přímky, které neleží ve stejné rovině a proto se neprotínají i když mají různý směr.
Poloha přímek v rovině je speciálním případem polohy přímek v prostoru.
Dvě přímky zadané obecnými rovnicemi tvoří soustavu
a
1
x
+
b
1
y
+
c
1
z
+
d
1
=
0
{\displaystyle a_{1}x+b_{1}y+c_{1}z+d_{1}=0}
a
2
x
+
b
2
y
+
c
2
z
+
d
2
=
0
{\displaystyle a_{2}x+b_{2}y+c_{2}z+d_{2}=0}
a
3
x
+
b
3
y
+
c
3
z
+
d
3
=
0
{\displaystyle a_{3}x+b_{3}y+c_{3}z+d_{3}=0}
a
4
x
+
b
4
y
+
c
4
z
+
d
4
=
0
{\displaystyle a_{4}x+b_{4}y+c_{4}z+d_{4}=0}
Tyto dvě přímky se protínají v jednom bodě právě tehdy, když platí
|
a
1
b
1
c
1
d
1
a
2
b
2
c
2
d
2
a
3
b
3
c
3
d
3
a
4
b
4
c
4
d
4
|
=
0
{\displaystyle {\begin{vmatrix}a_{1}&b_{1}&c_{1}&d_{1}\\a_{2}&b_{2}&c_{2}&d_{2}\\a_{3}&b_{3}&c_{3}&d_{3}\\a_{4}&b_{4}&c_{4}&d_{4}\end{vmatrix}}=0}
Máme-li dvě přímky vyjádřené vztahy
y
=
m
1
x
+
q
1
{\displaystyle y=m_{1}x+q_{1}}
z
=
n
1
x
+
r
1
{\displaystyle z=n_{1}x+r_{1}}
y
=
m
2
x
+
q
2
{\displaystyle y=m_{2}x+q_{2}}
z
=
n
2
x
+
r
2
{\displaystyle z=n_{2}x+r_{2}}
Pak podmínku, aby se tyto přímky proťaly lze zapsat
q
1
−
q
2
r
1
−
r
2
=
m
1
−
m
2
n
1
−
n
2
{\displaystyle {\frac {q_{1}-q_{2}}{r_{1}-r_{2}}}={\frac {m_{1}-m_{2}}{n_{1}-n_{2}}}}
Pro souřadnice průsečíku pak platí
x
P
=
q
2
−
q
1
m
1
−
m
2
=
r
2
−
r
1
n
1
−
n
2
{\displaystyle x_{P}={\frac {q_{2}-q_{1}}{m_{1}-m_{2}}}={\frac {r_{2}-r_{1}}{n_{1}-n_{2}}}}
y
P
=
m
1
q
2
−
m
2
q
1
m
1
−
m
2
{\displaystyle y_{P}={\frac {m_{1}q_{2}-m_{2}q_{1}}{m_{1}-m_{2}}}}
z
P
=
n
1
r
2
−
n
2
r
1
n
1
−
n
2
{\displaystyle z_{P}={\frac {n_{1}r_{2}-n_{2}r_{1}}{n_{1}-n_{2}}}}
Pokud se takové přímky protínají, pak jejich odchylku
φ
{\displaystyle \varphi }
cos
φ
=
|
1
+
m
1
m
2
+
n
1
n
2
|
(
1
+
m
1
2
+
n
1
2
)
(
1
+
m
2
2
+
n
2
2
)
{\displaystyle \cos \varphi ={\frac {\left|1+m_{1}m_{2}+n_{1}n_{2}\right|}{\sqrt {(1+m_{1}^{2}+n_{1}^{2})(1+m_{2}^{2}+n_{2}^{2})}}}}
Podmínku rovnoběžnosti přímek lze pak vyjádřit jednoduchými vztahy
m
1
=
m
2
{\displaystyle m_{1}=m_{2}}
n
1
=
n
2
{\displaystyle n_{1}=n_{2}}
kolmé , je-li splněna podmínka
1
+
m
1
m
2
+
n
1
n
2
=
0
{\displaystyle 1+m_{1}m_{2}+n_{1}n_{2}=0}
Mějme přímky vyjádřeny rovnicemi
x
−
x
1
cos
α
1
=
y
−
y
1
cos
β
1
=
z
−
z
1
cos
γ
1
{\displaystyle {\frac {x-x_{1}}{\cos \alpha _{1}}}={\frac {y-y_{1}}{\cos \beta _{1}}}={\frac {z-z_{1}}{\cos \gamma _{1}}}}
x
−
x
2
cos
α
2
=
y
−
y
2
cos
β
2
=
z
−
z
2
cos
γ
2
{\displaystyle {\frac {x-x_{2}}{\cos \alpha _{2}}}={\frac {y-y_{2}}{\cos \beta _{2}}}={\frac {z-z_{2}}{\cos \gamma _{2}}}}
Odchylka těchto přímek se určí jako
cos
φ
=
cos
α
1
cos
α
2
+
cos
β
1
cos
β
2
+
cos
γ
1
cos
γ
2
{\displaystyle \cos \varphi =\cos \alpha _{1}\cos \alpha _{2}+\cos \beta _{1}\cos \beta _{2}+\cos \gamma _{1}\cos \gamma _{2}}
Podmínku rovnoběžnosti takovýchto přímek lze zapsat rovnicemi
cos
α
1
=
cos
α
2
,
cos
β
1
=
cos
β
2
,
cos
γ
1
=
cos
γ
2
{\displaystyle \cos \alpha _{1}=\cos \alpha _{2},\cos \beta _{1}=\cos \beta _{2},\cos \gamma _{1}=\cos \gamma _{2}}
kolmosti lze vyjádřit jako
cos
α
1
cos
α
2
+
cos
β
1
cos
β
2
+
cos
γ
1
cos
γ
2
=
0
{\displaystyle \cos \alpha _{1}\cos \alpha _{2}+\cos \beta _{1}\cos \beta _{2}+\cos \gamma _{1}\cos \gamma _{2}=0}
Vzdálenost
δ
{\displaystyle \delta }
mimoběžných přímek udává vztah
δ
=
|
|
x
1
−
x
2
y
1
−
y
2
z
1
−
z
2
cos
α
1
cos
β
1
cos
γ
1
cos
α
2
cos
β
2
cos
γ
2
|
|
cos
β
1
cos
γ
1
cos
β
2
cos
γ
2
|
2
+
|
cos
γ
1
cos
α
1
cos
γ
2
cos
α
2
|
2
+
|
cos
α
1
cos
β
1
cos
α
2
cos
β
2
|
2
|
{\displaystyle \delta =\left|{\frac {\begin{vmatrix}x_{1}-x_{2}&y_{1}-y_{2}&z_{1}-z_{2}\\\cos \alpha _{1}&\cos \beta _{1}&\cos \gamma _{1}\\\cos \alpha _{2}&\cos \beta _{2}&\cos \gamma _{2}\end{vmatrix}}{\sqrt {{\begin{vmatrix}\cos \beta _{1}&\cos \gamma _{1}\\\cos \beta _{2}&\cos \gamma _{2}\end{vmatrix}}^{2}+{\begin{vmatrix}\cos \gamma _{1}&\cos \alpha _{1}\\\cos \gamma _{2}&\cos \alpha _{2}\end{vmatrix}}^{2}+{\begin{vmatrix}\cos \alpha _{1}&\cos \beta _{1}\\\cos \alpha _{2}&\cos \beta _{2}\end{vmatrix}}^{2}}}}\right|}
Vzájemná poloha přímek daných parametrickými rovnicemi