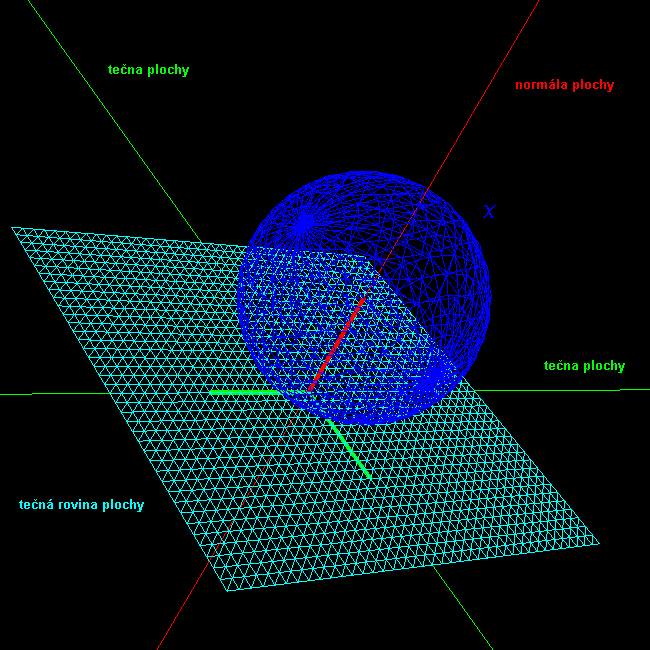
Geometrie/Tečný vektor, tečná rovina a tečna plochy

Z Wikiknih

[editovat] Definice

Nechť je plocha χ dána vektorovou rovnicí

,

a nechť k je křivka ležící na této ploše popsaná vektorovou rovnicí

.

Zvolme si na této křivce pevný bod G(t₀). Potom g(t₀) je tečný vektor plochy χ v bodě G(t₀). Přímka určená tečným vektorem procházející tímto bodem se nazývá tečna plochy χ v bodě G(t₀). Nechť k₁ je u¹-křivka a k₂ je u²-křivka plochy χ. Označme P jejich průsečík. Potom tečný vektor křivky k₁ v bodě P je roven parciální derivaci f₁, a tečný vektor křivky k₂ je v tomto bodě roven parciální derivaci f₂. Jelikož f₁ a f₂ jsou lineárně nezávislé, tvoří rovinu. Všechny přímky, které jsou tečnami plochy v daném bodě leží v této rovině, která se nazývá tečná rovina.

[editovat] Algoritmus

public static Surface TecnaRovina(Surface plocha, double u, double v)
{
  Point3d f=plocha.GetValue(u,v);
  return new PlaneSurface(f,plocha.PartialDerivU(u,v),plocha.PartialDerivV(u,v));
 //vrací rovinu určenou bodem f a prvními parciálními derivacemi v tomto bodě
}