Geometrie/Úvod do křivek
Úvod do křivek
[editovat | editovat zdroj]Popis
[editovat | editovat zdroj]Jedním z klíčových problémů počítačové vědy je vstup dat. Cesty, jimiž se data do počítačů mohou dostat, jsou v zásadě dvě. První cestou je generování dat přímo počítačem. Druhým způsobem je fyzické vkládání dat za pomocí nějakého vstupního zařízení. Druhý způsob je zřejmě velice náročný, je tedy přirozenou snahou tuto činnost zefektivnit.
Problém vstupu dat je obzvláště markantní v počítačové grafice. Pro většinu operací s objekty v počítači je nutné jejich exaktní vymezení. Objekty v počítačové grafice jsou obyčejně množiny bodů, které jsou omezeny plochami, případně v rovině křivkami (pokud se nejedná o fraktály, u nichž je problematické vymezení pojmů jako dimenze, délka atp.). Je tedy přirozeným požadavkem zjednodušit vstup právě křivek a ploch. Křivky a plochy jsou nejlépe reprezentovány funkcemi a funkce je problematické zadávat. Bylo by absurdní chtít po uživateli, aby zadal funkci ve tvaru y = f (x1, x2, . . . , xn) a měl představu o jejím tvaru. Hledají se tedy metody, které umožní uživateli co nejjednodušeji zadat nějakou křivku, či plochu, a to pokud možno tak aby byl dopředu odhadnutelný její tvar. Uživatel má obyčejně za úkol zadat jen několik řídicích bodů a matematický aparát (od kterého je odstíněn) se o vytvoření křivky postará sám.
V roce 1959 používal P. de Casteljau u firmy Citröen matematický model křivek a ploch, jenž mu je umožňoval jednoduše zadávat. Podobně roku 1961 P. Béziere používal program UNISURF u firmy Renault. V té době byla ještě stále tato disciplína integrální součástí počítačové grafiky. V sedmdesátých letech se stále zřetelněji vyčleňovala, až si vysloužila vlastní název: CAGD jako součást A. R. Forrestem zavedené disciplíny zvané výpočetní geometrie. Metody CAGD se postupem času zdokonalovaly a v současné době je k dispozici velmi silný nástroj, který je stále aktivně rozvíjen. Podstatou tohoto rozvoje je poměrně kvalitní matematický aparát (částečně převzatý z deskriptivní geometrie) a v neposlední řadě zřetelný komerční efekt..
Výraznou změnu do CAGD vneslo používání racionálních Bézierových křivek (a ploch) a zvláště jejich speciální případ, racionální Bézierovy křivky s neuniformní parametrizací, tzv. NURBS. Tyto metody umožňují generovat klasické geometrické prvky (jako jsou koule, válce, kuželosečky atp.) za pomoci metod aproximace
Vyjádření křivek
[editovat | editovat zdroj]Křivky jsou obyčejně v počítači reprezentovány jako soustava parametrů nějaké rovnice, která je posléze generativně zobrazována. Toto vyjádření může být v podstatě trojího druhu: Explicitní, Implicitní, Parametrické
Explicitně vyjádřená křivka je zadána jako funkce ve tvaru:
Derivace v obecném bodě x se spočítá podle vztahu
Implicitní zadání křivky má tvar:
Toto zadání není příliš vhodné pro potřeby počítačové grafiky, neboť neumožňuje postupný výpočet křivky. Svůj význam má například při výpočtu průsečíků s implicitně zadanou křivkou (v trojrozměrném prostoru).
V počítačové grafice se nejčastěji pro vyjádření křivek používá tvar parametrický:
Parametrické vyjádření se jednoduše zapisuje vektorově:
Derivace křivky vyjádřené parametricky má tvar
Derivuje se tedy po jednotlivých složkách. Parametr t se pohybuje v intervalu < 0,1 >.
Modelování křivek
[editovat | editovat zdroj]Základním prvkem teorie křivek v počítačové grafice jsou křivky polynomiální (Pn(t) = a0 + alt + ... + antn). Z nich se skládají křivky po částech polynomiální, to jsou křivky jejichž segmenty jsou polynomiálními křivkami. Nejčastěji používané jsou křivky třetího stupně - kubiky, které poskytují dostatečně širokou škálu tvarů. Jejich výpočet bývá nenáročný, jsou snadno manipulovatelné a je možné u nich zaručit spojitost C2, požadovanou někdy při modelování v CAD systémech. Křivky vyššího stupně mohou způsobovat nežádoucí vlnění a oscilace a jsou náročnější na výpočet.
Modelování probíhá obyčejně tak, že je definováno několik řídicích bodů (řídicí polygon) a matematický aparát z jejich polohy určí průběh křivky. Některé metody umožňují zadávání křivek též pomocí tečných vektorů, je možno klást podmínky na hladkost navázání aj.
Existují dva základní druhy interpretace řídicích bodů a to interpolace a aproximace. Při interpolaci (Obr. 1.3) generovaná křivka probíhá danými body, zatímco při aproximaci je řídicími body tvar křivky určen, ta jimi však procházet nemusí.
Interpolační křivky
[editovat | editovat zdroj]Na intervalu I je dána uspořádaná n-tice tzv. opěrných bodů:
Interpolační funkce je funkce f, jež splňuje požadavek
Interpolační křivka k dané množině bodů je tedy taková křivka, která jimi prochází.
Interpolace polynomem
[editovat | editovat zdroj]V praxi je nejčastější interpolační technikou interpolace polynomem, a to bud' jediným polynomem n -1 řádu pro n bodů, nebo po částech.
Interpolace jediným polynomem
[editovat | editovat zdroj]Interpolace polynomem m-tého řádu znamená najít řešení soustavy rovnic
Vstupem této rovnice jsou body zadané souřadnicemi pro od 1 do n. Těmito body má křivka procházet a řešením soustavy dostaneme koeficienty polynomu . Tento polynom má tvar
Příliš velký stupeň polynomu může vnutit křivce nepřirozené zvlnění. V počítačové praxi bývá polynomiální interpolace používána pro křivky stupně maximálně pět.
Interpolace po částech
[editovat | editovat zdroj]Daleko častější interpolační technikou je interpolace křivky po jejích částech.
Uvažujme n-tici bodů. Aproximací polynomem třetího řádu potom rozumíme aproximaci jejích každých čtyř bodů polynomem třetího stupně. Problémem, který je potřeba řešit, je potom navazování křivky v bodech, kde jedna část přechází v druhou. Existuje několik metod, které řeší navazování v těchto bodech automaticky. Akimova interpolace, interpolace Hermitovskými polynomy (jejíž zvláštním případem jsou Fergusonovy kubiky, které se používají i pro aproximace a konečně spline křivky k-tého řádu, které zaručují spojitost k-1 řádu.
Interpolační metody nejsou pro výše uvedené nevýhody příliš často v počítačové grafice využívány. Tyto metody nacházejí uplatnění v numerické matematice a v matematické statistice, kde se na základě interpolací usuzuje na potenciální chování nějakých jevů v budoucnu (potom se hovoří o extrapolaci). Tyto metody z těchto oborů také původně vzešly.
Aproximační křivky
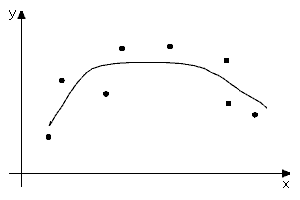
[editovat | editovat zdroj]Aproximací bodů rozumíme vytvoření takové křivky, která je těmito body vhodně řízena. Není kladen požadavek na procházení opěrnými body (ani prvním a posledním bodem). Způsob řízení odpovídá vytváření této křivky. Existuje v zásadě dvojí přístup k aproximacím.
Přístup první je znám z numerické matematiky a jeho cílem je smysluplná interpretace vstupních dat. Uveďme metodu nejmenších čtverců, její smyslem je nalézt křivku, jež je hladká, a čtverec vzdálenosti řídicích bodů od ní je minimální. Neměnným základem těchto postupů jsou zadané body. Generovaná křivka má jen informativní charakter.
Druhý přístup je používán v počítačové grafice. Smyslem není interpretace bodů, ale generování křivky. Křivka může být řízena body, potom hovoříme o tzv. řídicím polygonu nebo body a vektory. Metoda, která křivku vytváří, zaručuje její vlastnosti. Požadované vlastnosti jsou její hladkost, spojitost, počet inflexí aj. Tyto metody byly navrženy tak, aby vyhovovaly technické praxi, a zaručují tedy například nízké tření navržených objektů aj.
V počítačové grafice se nejčastěji používá aproximace po částech (podobně jako interpolace), a to obyčejně kubikami (tedy křivkami, které jsou generovány polynomy třetího řádu). Důvody pro to jsou dva. Kubiky jsou dostatečně "pružnými" křivkami, aby se jimi dalo vyjádřit téměř vše, co je v praxi potřeba. Dalším důležitým faktorem je, že stupeň polynomu tři umožňuje velmi rychlý výpočet výsledné křivky, což je výhodné pro její interaktivní tvorbu.
Parametricky lze danou kubiku Q(t) vyjádřit ve tvaru:
můžeme zapsat zkráceně v maticovém tvaru:
Derivaci q'(t) získáme derivací vektoru T
Konstantní matici C můžeme rozepsat do součinu
kde matice M je typu 4x4 a nazývá se bázová matice. Čtyřprvkový vektor se nazývá geometrický vektor. Geometrický vektor reprezentuje vliv vnějších parametrů. Obsahuje řídicí body nebo řídicí body a tečné vektory atp. Bázová matice, která je dána použitou metodou,pak určuje výpočet křivky podle vztahu:
Mezi často požadované vlastnosti křivek patří:
1. Invariance k afinním transformacím a projekcím, která zaručuje, že například rotace řídicího polygonu a následné generování křivky má stejný výsledek, jako rotace každého bodu z vygenerované křivky.
2. Vlastnost konvexní obálky (angl. convex hull property)
- silná podmínka - celá křivka leží v konvexní obálce všech svých řídicích bodů,
- slabá podmínka - část křivky leží v konvexní obálce některých řídicích bodů (typicky segment, v obálce svého generujícího polygonu).
3. Lokalita změn - změnou polohy (u racionálních křivek i váhy) řídicího bodu se mění jen část křivky, nikoli křivka celá
4. Křivka může procházet krajními body svého řídicího polygonu.
Spojitost
[editovat | editovat zdroj]Při navazování oblouků je významným faktorem spojitost křivek. Říkáme, že výsledná křivka je spojitá, pokud je spojitá ve všech svých bodech, a tedy zejména v navazovacích bodech. Křivka je hladká, pokud jsou ve všech jejích bodech spojité i její první derivace. Pro vyšší derivace říkáme, že křivka má spojitost druhého, třetího a obecně n-tého řádu.
Říkáme, že křivka Q(t) je třídy , má-li ve všech bodech spojité derivace do řádu n. Označení Cn se nazývá parametrická spojitost.
Dva segmenty jsou spojitě navázány (neboli mají spojení třídy , ), pokud je koncový bod prvního segmentu počátečním bodem segmentu druhého. Dva segmenty mají spojení , , pokud je tečný vektor v koncovém bodě segmentu , roven tečnému vektoru , v jeho počátečním bodě. Analogicky rovnost vektoru první a druhé derivace je požadována pro , (Obr. 1.4) atd.
Zkráceně zapisujeme:
Čím vyšší spojitost je požadována, tím delší "dobu" (ve smyslu parametru t) se oba segmenty k sobě přimykají. Zjevně . Ze spojitosti plyne, že bod se pohybuje po spojité dráze, ale v uzlu může měnit skokem směr pohybu, rychlost i zrychlení. Směr pohybu a velikost rychlosti se nemůže měnit skokem při spojitosti a zrychlení zůstává nezměněné při spojitosti .
Pohybující se bod v uzlu nemůže změnit skokem směr, ale může skokem změnit rychlost.

Obr. 1.6 Geometrická a parametrická spojitost. Lupa ukazuje tečné vektory
Opticky zaručuje . spojitost "skoro stejnou" hladkost jako ., z hlediska použití bývá daleko snazší zaručit spojitost . nežli .
Autoři
[editovat | editovat zdroj]Tento text vypracovali studenti Univerzity Palackého v Olomouci katedry Matematické informatiky jako zápočtový úkol do předmětu Počítačová geometrie.








![{\displaystyle P(t)=[x(t),y(t)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fc0a761b20e7f8ab4dca6b64eaaaadf0bd78bfe9)
![{\displaystyle P'(t)=[x'(t),y'(t)]=[{\frac {dx(t)}{dt}},{\frac {dy(t)}{dt}}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d2b1e710f8a567dc7dba66aecc73eaf2face74b0)




![{\displaystyle [x_{i},y_{i}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f18fba919c21da790d4b17ab87121634ee53d30b)






![{\displaystyle Q(t)=TC=[t^{3},t^{2},t,1]{\begin{vmatrix}a_{x}&a_{y}&a_{z}\\b_{x}&b_{y}&b_{z}\\c_{x}&c_{y}&c_{z}\\d_{x}&d_{y}&d_{z}\\\end{vmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9ec6c56417dbc312a7f9b243fcdebd870f46a91f)
![{\displaystyle q'(t)={\frac {d}{dt}}q(t)={\frac {d}{dt}}TC=[3t^{2},2t,1,0]C}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c297688bec8da42f9dde37fe17b45ede53c07c82)

![{\displaystyle Q(t)=[x(t),y(t),z(t)]=[t^{3},t^{2},t,1]{\begin{vmatrix}m_{11}&m_{12}&m_{13}&m_{14}\\m_{21}&m_{22}&m_{23}&m_{24}\\m_{31}&m_{32}&m_{33}&m_{34}\\m_{41}&m_{42}&m_{43}&m_{44}\\\end{vmatrix}}{\begin{vmatrix}G_{1}\\G_{2}\\G_{3}\\G_{4}\\\end{vmatrix}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/913a4265030f3a5880facfa1b279ac99f7255f51)










