Úvod do algebry/Polynomy

Z Wikiknih

Přejít na: navigace, hledání

Obsah

[editovat] Co je to polynom?

Polynom neboli mnohočlen je výraz sestávající jen ze součtů (rozdílů), násobků a celočíselných mocnin proměnných. Obecný polynom může vypadat třeba takto:

P(x, y, z) = 2 x^2 y z^3 - 3.1 y^2 + 5 y z - 2 \,

V dalším textu se ale budeme zabývat jen polynomy jedné proměnné x, které můžeme zapsat v obecném tvaru:

P(x) = A_{0} x^n + A_{1} x^{n-1} + ... + A_{n-1} x^1 + A_{n} \,

Nebo profesionálněji:

P(x) = \sum_{i=0}^n A_{i} x^{n-i}

Konstanty A0 až An jsou koeficienty a může se jednat o libovolná reálná nebo komplexní čísla.

[editovat] Stupeň polynomu

Nejvyšší exponent s nenulovou hodnotou v polynomu určuje jeho stupeň. V uvedeném příkladu má polynom stupeň n.

Polynom P(x)=0 se nazývá nulový polynom a jeho stupeň položíme roven -1.

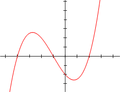
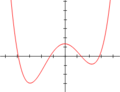
Polynom stupně 0 je (nenulová) konstanta. Graf polynomu stupně 1 je přímka, polynomu stupně 2 parabola apod.

Graf polynomu 2.

3.

4.

a 5. stupně

[editovat] Kořeny polynomu

Kořen polynomu P je takové číslo x, pro které má P(x) hodnotu 0.

Polynom prvního stupně má vždy 1 kořen, neboť vždy lze snadno nalézt takové x, pro které platí:

A_{0} x + A_{1} = 0 \,

Jak známo, polynom druhého stupně (kvadratická funkce) má dvě, jedno nebo žádné řešení v oboru reálných čísel. To odpovídá buď dvěma reálným, jednomu reálnému dvojnásobnému nebo dvěma komplexním kořenům (komplexně sdruženým).

Polynom stupně n má nejméně 1 a nejvýše n různých kořenů.

Pozn: Pokud má polynom

  • všechny koeficienty reálné a
  • některé kořeny komplexní,

jsou všechny komplexní kořeny komplexně sdružené se svým protějškem. (Tzn. mají vzájemně shodnou reálnou, ale opačnou imaginární hodnotu.) Pokud má polynom obecně komplexní koeficienty(y), jsou jeho kořeny v obecném případě komplexní a nejsou komplexně sdružené.

[editovat] Bezoutova věta

Předpokládejme, že P(x) je libovolný polynom stupně vyššího než 1; dále, že y je libovolné číslo. Pak lze najít polynom Q

P(x) = (x − y).Q(x) + P(y)

Polynom Q(x) má stupeň o 1 nižší než P(x).

[editovat] Rozklad polynomu na kořenové činitele

Nenulové polynomy reálnými koeficienty lze vyjádřit také jako součin kořenových činitelů, a to ve tvaru

P(x) = (x - k_{1})^{s_{1}} . (x - k_{2})^{s_{2}} . ... . (x - k_{n-1})^{s_{n-1}} . k_{n}

kde k1 až kn jsou jednotlivé kořeny a s1 až sn − 1 jejich příslušné násobnosti.

Podobná operace se dá provést i u polynomů s komplexními koeficienty.

Převedení součinu kořenových činitelů na standardní tvar polynomu je maličkost, stačí je roznásobit. Opačný převod je výrazně těžší:

  • U polynomu nulového nebo s nulovým stupněm nemá smysl se o kořenovém činiteli bavit.
  • Polynom stupně 1 už de facto v tomto tvaru je.
  • Pro polynom 2. stupně použijeme známou rovnici
x_1 = \frac{-b + \sqrt {b^2-4ac}}{2a} a \ x_2 = \frac{-b - \sqrt {b^2-4ac}}{2a},

a nenecháme se odradit odmocňováním záporných čísel.

  • Rozklad polynomů vyšších stupňů už je v obecném případě dosti náročný až (od 5. stupně) analyticky nemožný.
Citováno z „http://cs.wikibooks.org/wiki/%C3%9Avod_do_algebry/Polynomy“